218. The Skyline Problem
The Skyline Problem
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return to the skyline formed by these buildings collectively.
The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:
leftiis the x coordinate of the left edge of theithbuilding.rightiis the x coordinate of the right edge of theithbuilding.heightiis the height of theithbuilding.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at a height 0.
The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]
Example 1:
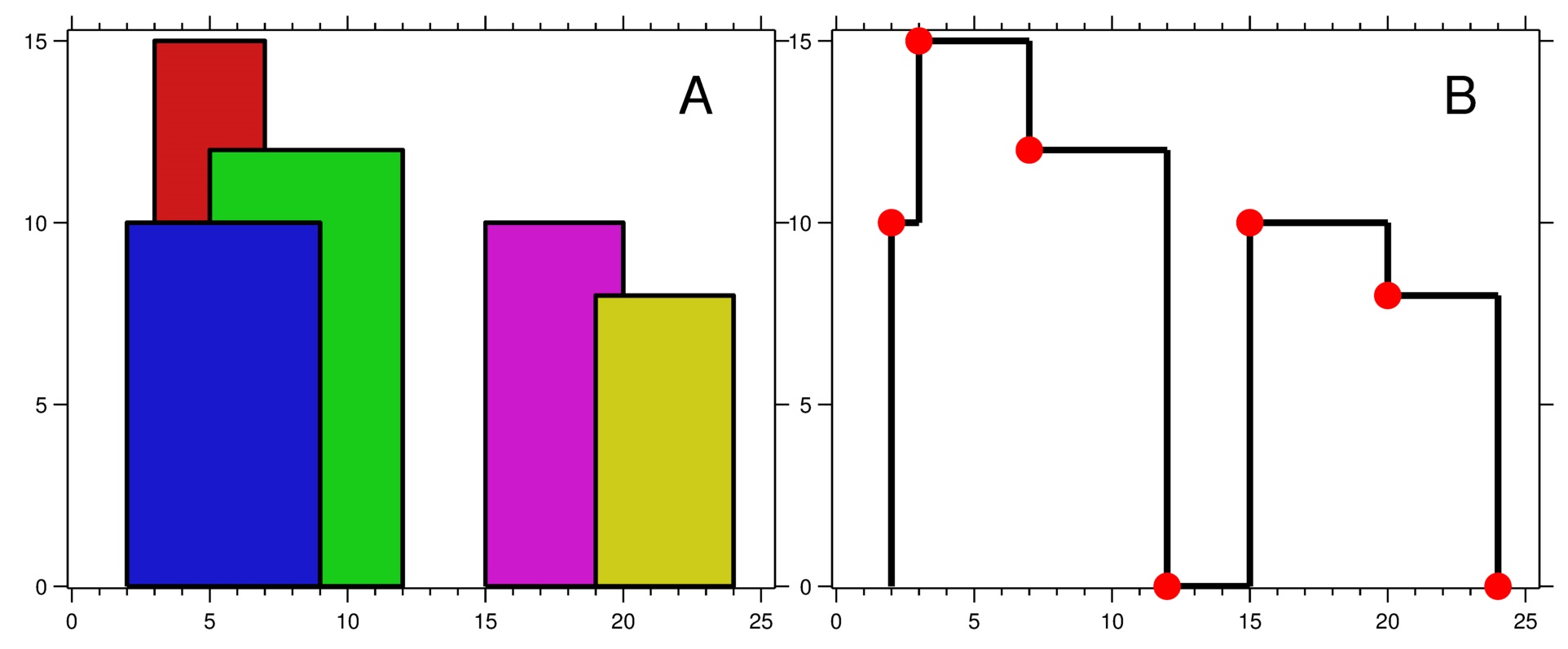
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]] Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]] Explanation: Figure A shows the buildings of the input. Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.
Example 2:
Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]] Constraints:
1 <= buildings.length <= 1040 <= lefti < righti <= 231 - 11 <= heighti <= 231 - 1buildingsis sorted byleftiin non-decreasing order.
- using Brute Force, O(N^2)
- using custom Heap class that takes a comparator function O(nlogn)
- using Divide and Conquer O(nlogn)
- using UnionFind (adapted to denote Right-Most edge as root for a range that was already updated with height info from taller buildings)
Approach) Brute force
/**
* @param {number[][]} buildings
* @return {number[][]}
*/
var getSkyline = function(buildings) {
var res=[], x=[],t=0;
buildings.forEach(v=>(x.push(v[0]),x.push(v[1])));
for (let c of x.sort((a,b)=>a-b)) if (res[res.length-1]?.[1]!==(t=buildings.reduce( (m,[b,e,h]) => b<=c && c<e && h>m? h: m,0))) res.push([c,t]);
return res;
};var getSkyline = function(buildings) {
let res = [];
let coordinates = [];
let heights = [];
for (let building of buildings) {
coordinates.push([building[0],building[2]]);
coordinates.push([building[1],-building[2]]);
}
//coordinates.sort((a,b)=>(b[1]-a[1]));
//coordinates.sort((a,b)=>(a[0]-b[0]));
//[[0,12,3],[1,8,4],[1,5,3],[2,5,3]]
coordinates.sort((a,b) => a[0]>b[0]?1: a[0]===b[0]? b[1]-a[1]: -1);
for (let coordinate of coordinates){
if(coordinate[1]>0)heights.push(coordinate[1]);
else heights.splice(heights.indexOf(-coordinate[1]),1);
console.log(coordinate,heights);
//spread operator on Math.max(...[]) or Math.max() => -infinity to ensure multiple max of max of max operation is successful. https://dmitripavlutin.com/javascript-math-max-infinity/
let cur =(heights.length == 0?0:Math.max(...heights));
if(res[res.length-1]?.[1]!==cur) res.push([coordinate[0], cur]);
}
return res;
};var getSkyline = function(buildings) {
let res = [];
let coordinates = [];
let heights = [];
for (let building of buildings) {
coordinates.push([building[0],0,building[2]]);
coordinates.push([building[1],1,building[2]]);
}
//[[0,12,3],[1,8,4],[1,5,3],[2,5,3]]
// must sort by: if point x has both start and end , process start point first (because we want to maintain a max height that includes new start point), if point x has multiple start points, process the highest point first (eg two buildings starts at point x at the very beginning), if point x has multiple end points, process the smallest point first (because we don't want to detect a height change and record it prematurely)
coordinates.sort((a,b) => a[0]===b[0]? (b[1]===a[1]?(b[1]===0?1:-1)*(b[2]-a[2]):a[1]-b[1]): a[0]-b[0]);
//console.log(coordinates);
for (let coordinate of coordinates){
if(!coordinate[1])heights.push(coordinate[2]);
else heights.splice(heights.indexOf(coordinate[2]),1);
//console.log(coordinate,heights);
let cur =(heights.length == 0?0:Math.max(...heights));
if(res[res.length-1]?.[1]!==cur) res.push([coordinate[0], cur]);
}
return res;
};
ORvar getSkyline = function(buildings) {
let res = [];
let coordinates = [];
let heights = [];
for (let building of buildings) {
coordinates.push([building[0],building[2]]);
coordinates.push([building[1],-building[2]]);
}
//coordinates.sort((a,b)=>(b[1]-a[1])); //coordinates.sort((a,b)=>(a[0]-b[0]));
//[[0,12,3],[1,8,4],[1,5,3],[2,5,3]]
coordinates.sort((a,b) => a[0]>b[0]?1: a[0]===b[0]? b[1]-a[1]: -1);
for (let coordinate of coordinates){
if(coordinate[1]>0)heights.push(coordinate[1]);
else heights.splice(heights.indexOf(-coordinate[1]),1);
console.log(coordinate,heights);
//spread operator on Math.max(...[]) or Math.max() => -infinity to ensure multiple max of max of max operation is successful. https://dmitripavlutin.com/javascript-math-max-infinity/
let cur =(heights.length == 0?0:Math.max(...heights));
if(res[res.length-1]?.[1]!==cur) res.push([coordinate[0], cur]);
}
return res;
};
Approach) Line Sweeping + Priority Queue (Max Heap)
var getSkyline = function(buildings) {
var res=[], x=[],heap= new Heap( {comparator:(a,b)=> a[0]-b[0]})
heap.heappush([0,Number.POSITIVE_INFINITY]);
buildings.forEach(v=>(x.push([v[0],v[1],v[2]]),x.push([v[1],0,v[2]])));
for (let [c,e,h] of x.sort((a,b)=>a[0]===b[0]? Math.sign(b[1])===Math.sign(a[1])? a[1]===0? a[2]-b[2]:b[2]-a[2] : b[1]-a[1] :a[0]-b[0]) ) {
if (e) heap.heappush([h,e]);
else while (heap.peek()[1]<=c) heap.heappop();
if(res[res.length-1]?.[1]!==heap.peek()[0]) res.push([c,heap.peek()[0]]);
}
return res;
};Approach) Divide & Conquer
var getSkyline = function(buildings) {
function dnc(b,e) {
if (b==e) return [[buildings[b][0],buildings[b][2]],[buildings[b][1],0]];
let left=dnc(b,b+Number.parseInt((e-b)/2)), right=dnc(b+Math.floor((e-b)/2)+1,e), res=[], lp=0, rp=0, le=left.length-1, re=right.length-1 , lch=[0,0],rch=[0,0],cur;
while (lp<=le && rp<=re) {
if (left[lp][0]<right[rp][0]) {
cur=[left[lp][0],Math.max(rch[1],left[lp][1])];
lch=left[lp++];
} else if (left[lp][0]>right[rp][0]) {
cur=[right[rp][0],Math.max(lch[1],right[rp][1])];
rch=right[rp++];
}
else {
cur=[right[rp][0],Math.max(left[lp][1],right[rp][1])];
lch=left[lp++],rch=right[rp++];
}
if (res[res.length-1]?.[1]!==cur[1]) res.push(cur);
}
while (lp<=le) res.push(left[lp++]) ;
while (rp<=re) res.push(right[rp++]) ;
return res;
}
return dnc(0,buildings.length-1);
};Approach) Brute Force with Heights array
var getSkyline = function(buildings) {
var set=new Set(), map=new Map();
buildings.forEach( v=> (set.add(v[0]),set.add(v[1])));
var points=Array.from(set.values()).sort((a,b)=>a-b);
points.forEach((v,i)=>map.set(v,i));
var res=[],heights=Array(points.length).fill(0);
for (let [b,e,h] of buildings) {
for (let i=map.get(b); i<map.get(e); ++i) heights[i]=Math.max(heights[i],h);
}
heights.forEach( (h,i) => res[res.length-1]?.[1]!==h? res.push([points[i],h]):null);
return res;
}Approach) Union Find Based on Brute Force with heights array
var getSkyline = function(buildings) {
var set=new Set(), map=new Map();
buildings.forEach( v=> (set.add(v[0]),set.add(v[1])));
var points=Array.from(set.values()).sort((a,b)=>a-b);
points.forEach((v,i)=>map.set(v,i));
var res=[],heights=Array(points.length).fill(0),uf=new UnionFind(points.length);
for (let [b,e,h] of buildings.sort((a,b)=>b[2]-a[2])) {
let left=uf.find(map.get(b)), right=map.get(e);
for (; left<right;) {
if (heights[left]===0) {
heights[left]=h
uf.union(left,right);
}
left=uf.find(++left);
}
}
heights.forEach( (h,i) => res[res.length-1]?.[1]!==h? res.push([points[i],h]):null);
return res;
}Implementation) Max Heap (PQ: Priority Queue)
class Heap { //max Heap
constructor ( {comparator}={comparator: (a,b)=>a-b}) {//changed for comparator
// Due to a completely balanced nature of the heap tree,
// the index of 1st element in current row/level indicates the # of elements in current row/level
this.size=0;
this.store=new Array(this.size+1); //1-based array for simplicity
this.comparator=comparator;//changed for comparator
}
static heapify(arr, {comparator}={comparator: (a,b)=>a-b} ) {
let heap=new Heap();
heap.store=arr; //in-place heapification
heap.size=arr.length;
// use 0-based array is actually faster because it eliminates shift
heap.store.unshift(null); //shift is O(n), but it simplifies a bit
for (let i=heap.size-Number.parseInt((heap.size+1)/2); i>0; --i) {
heap.#heapify(i);
}
return heap;
}
get queueSize() {
return this.size;
}
heappush(x) {
this.store[++this.size]=x;
this.#heapifyBottomUp(this.size);
}
#heapifyBottomUp(i) {
for (;i>1 && this.comparator(this.store[i], this.store[Math.floor(i/2)])>0;i=Number.parseInt(i/2) ) { //changed for comparator
[this.store[Math.floor(i/2)],this.store[i]]=[this.store[i],this.store[Number.parseInt(i/2)]];
}
}
peek() {
return this.size? this.store[1]:null;
}
heappop() {
if (this.size===0) return null;
let r=this.store[1];
this.store[1]=this.store[this.size--];
this.#heapify(1); // because i's both children are by themselves maxheap already (invariant/precondition)
return r;
}
#heapify(i) {
// it appears that this.store[i*2+1]??Number.NEGATIVE_INFINITE will cause bug if size already shrinked, use size check is safer
// after careful tests, it's proved that it won't cause bug
// this is because this.size-- occurs before #heapify(i) is called
// so there are two cases
// 1. this.size now points to left child: this.store[this.size+1] was copied to store[1] before entering #heapify(i)
// store[this.size+1]< its parent node, so even though i*2+1 is queried, it won't cause swapping and the bug won't surface
// 2. this.size now points to a right child: i*2<=this.size would have failed and skipped the bug
//for (;i*2<=this.size && this.store[i]< Math.max(this.store[i*2],this.store[i*2+1]??Number.NEGATIVE_INFINITE); ) {
// if (i*2+1>this.size) console.log('\nerror',i,'size',this.size,'arr=',this.store.length,this.store);
// if (this.store[i*2]===Math.max(this.store[i*2],this.store[i*2+1]??Number.NEGATIVE_INFINITE)) {
// the following two lines are changed to accomodate comparator input, note that we can no longer use Number.NEGATIVE_INFINITY as constant, we must substitute that with the same type of object that stored in the heap, thus swap them with this.store[i*2] when i*2+1 is out of bound
for (;i*2<=this.size && this.comparator(this.store[i], this.#max(this.store[i*2],i*2+1<=this.size?this.store[i*2+1]:this.store[i*2]))<0; ) { //changed for comparator
if (this.store[i*2]===this.#max(this.store[i*2],i*2+1<=this.size?this.store[i*2+1]:this.store[i*2]) ) { //changed for comparator
[this.store[i*2],this.store[i]]=[this.store[i],this.store[i*2]];
i*=2;
}
else {
[this.store[i*2+1],this.store[i]]=[this.store[i],this.store[i*2+1]];
i=i*2+1;
}
}
}
#max (a,b) { //changed for comparator
return this.comparator(a,b)>0? a:b;
}
}Implementation) Union Find
class UnionFind {
constructor (length) {
this.roots=Array.from(Array(length).keys());
}
union (left,right) { //no need to use rank, use path compression is enough, because we set parent to the right-most edge
this.roots[left]=this.find(right); // standard UnionFind lroot=find(left), rroot=find(right) and merge lroot and rroot with ranking considerations to compress path
}
find (a) { //path compression
var b=a;
while (this.roots[b]!==b) {
b=this.roots[b];
}
return this.roots[a]=b;
}
}That’s all folks! In this post, we solved LeetCode problem #218. The Skyline Problem
I hope you have enjoyed this post. Feel free to share your thoughts on this.
You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.
In this blog, I have tried to solve leetcode questions & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!


Comments
Post a Comment