623. Add One Row to Tree
Add One Row to Tree
Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.
Note that the root node is at depth 1.
The adding rule is:
- Given the integer
depth, for each not null tree nodecurat the depthdepth - 1, create two tree nodes with valuevalascur's left subtree root and right subtree root. cur's original left subtree should be the left subtree of the new left subtree root.cur's original right subtree should be the right subtree of the new right subtree root.- If
depth == 1that means there is no depthdepth - 1at all, then create a tree node with valuevalas the new root of the whole original tree, and the original tree is the new root's left subtree.
Example 1:
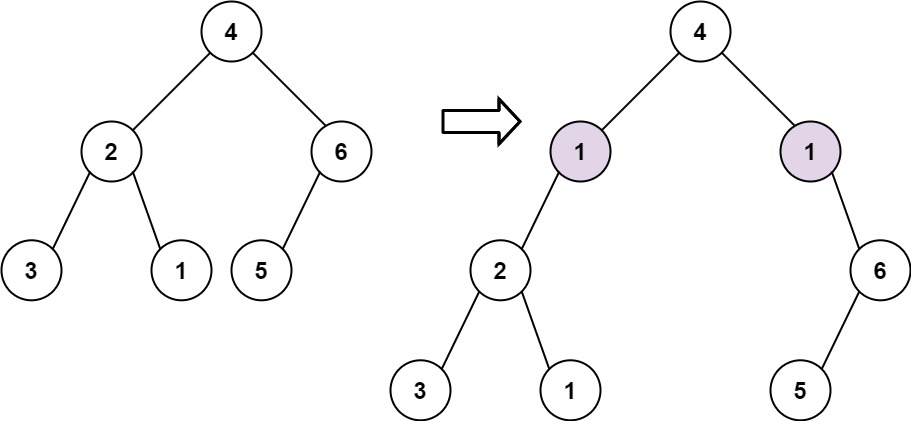
Input: root = [4,2,6,3,1,5], val = 1, depth = 2 Output: [4,1,1,2,null,null,6,3,1,5]
Example 2:
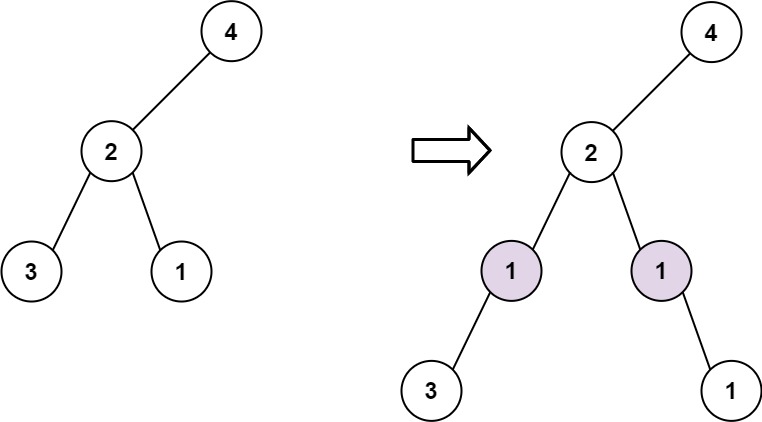
Input: root = [4,2,null,3,1], val = 1, depth = 3
Output: [4,2,null,1,1,3,null,null,1]Constraints:
- The number of nodes in the tree is in the range
[1, 104]. - The depth of the tree is in the range
[1, 104]. -100 <= Node.val <= 100-105 <= val <= 1051 <= depth <= the depth of tree + 1
Note:
- The given d is in the range [1, maximum depth of the given tree + 1].
- The given binary tree has at least one tree node.
This question allows us to add a row to the binary tree, giving the value that needs to be added, and the depth of the position that needs to be added. The example given in the question can also clearly illustrate the problem.
But one case is missed, that is, when depth =1, how should this be added? At this time, the root node needs to be replaced. The processing methods for other cases are the same. Here, the blogger’s first image thinks that it should be done by layer order traversal.
After traversing a layer, depth is decremented by 1. When depth ==1, it is necessary to traverse each node of the current layer.
First, use temporary variables to save its original left and right child nodes, then create a new left and right child node with a value of v, connect the original left child node to the left child node of the new left child node, and The original right child node is connected to the right child node of the new right child node, is it very round -.-|||.
If depth is not 1, then the original queue operation is traversed in the layer order. Remember to return directly when depth is detected to be 0 because the add operation has been completed, and there is no need to traverse the remaining nodes.
Code:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} val
* @param {number} depth
* @return {TreeNode}
*/
var addOneRow = function(root, val, depth, dir = 'left') {
if (depth === 1) {
const node = new TreeNode(val);
[root, node[dir]] = [node, root]
} else if (root) {
root.left = addOneRow(root.left, val, depth - 1, 'left')
root.right = addOneRow(root.right, val, depth - 1, 'right')
}
return root
};/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} val
* @param {number} depth
* @return {TreeNode}
*/
var addOneRow = function(root, val, depth) {
if (depth == 0 || depth == 1 ) {
let newRoot = new TreeNode(val);
depth ? newRoot.left = root : newRoot.right = root;
return newRoot;
}
if (root && depth > 1 ) {
root.left = addOneRow(root.left, val, depth > 2 ? depth - 1 : 1 );
root.right = addOneRow(root.right, val, depth > 2 ? depth - 1 : 0 );
}
return root;
};/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} v
* @param {number} d
* @return {TreeNode}
*/
var addOneRow = function (root, v, d) {
if (d === 1) {
let n = new TreeNode(v)
n.left = root
return n
}
r(root, 1)
return root
function r(n, depth) {
if (!n) return
if (depth === d - 1) {
{
let t = new TreeNode(v)
t.left = n.left
n.left = t
}
{
let t = new TreeNode(v)
t.right = n.right
n.right = t
}
return
}
r(n.left, depth + 1)
r(n.right, depth + 1)
}
};var addOneRow = function(root, val, depth, level=1, isRightTree=false) {
//edge case for if the depth is after a leaf node
if (!root && level === depth) return new TreeNode(val)
if (!root) return null
//If we are on a depth level, add the node and do not recursively call further nodes from this node
if (level === depth) {
let node = new TreeNode(val)
if (isRightTree) node.right = root
else node.left = root
return node
}
root.left = addOneRow(root.left, val, depth, level+1, false)
root.right = addOneRow(root.right, val, depth, level+1, true)
return root
};var addOneRow = function(root, val, depth) {
if(depth === 1){
let newRoot = new TreeNode(val);
newRoot.left = root;
return newRoot;
}
let queue = [root];
let level = 0;
while(queue.length !== 0){
level += 1
let numNodes = queue.length;
for(let i = 0; i < numNodes; i++){
let node = queue.shift();
if(node.left){
queue.push(node.left);
}
if(node.right){
queue.push(node.right);
}
if(level === depth - 1){
let newLeft = new TreeNode(val);
let newRight = new TreeNode(val);
newLeft.left = node.left;
newRight.right = node.right;
node.left = newLeft;
node.right = newRight;
}
}
}
return root;
};var addOneRow = function (root, val, depth) {
if (depth == 1) {
ans = new TreeNode(val);
ans.left = root;
return ans;
}
let step = 1;
let que = [root];
while (step < depth && que.length != 0) {
let size = que.length;
for (let i = 0; i < size; i++) {
let node = que.shift();
if (step == depth - 1) {
let leftPart = node.left;
let rightPart = node.right;
node.left = new TreeNode(val);
node.right = new TreeNode(val);
node.left.left = leftPart;
node.right.right = rightPart;
}
if (node.left) {
que.push(node.left);
}
if (node.right) {
que.push(node.right);
}
}
step++;
}
return root;
};That’s all folks! In this post, we solved LeetCode problem #623. Add One Row to Tree
I hope you have enjoyed this post. Feel free to share your thoughts on this.
You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.
In this blog, I have tried to solve leetcode questions & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!

Comments
Post a Comment