1335. Minimum Difficulty of a Job Schedule
Minimum Difficulty of a Job Schedule
You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).
You have to finish at least one task every day. The difficulty of a job schedule is the sum of the difficulties of each day of the d day. The difficulty of a day is the maximum difficulty of a job done on that day.
You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].
Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.
Example 1:
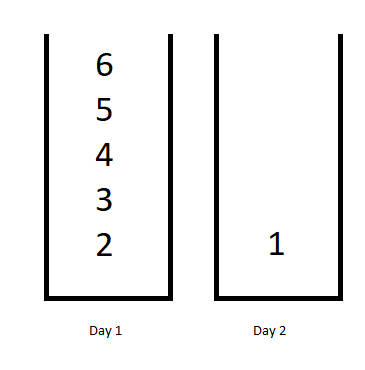
Input: jobDifficulty = [6,5,4,3,2,1], d = 2 Output: 7 Explanation: First day you can finish the first 5 jobs, total difficulty = 6. Second day you can finish the last job, total difficulty = 1. The difficulty of the schedule = 6 + 1 = 7
Example 2:
Input: jobDifficulty = [9,9,9], d = 4 Output: -1 Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
Example 3:
Input: jobDifficulty = [1,1,1], d = 3 Output: 3 Explanation: The schedule is one job per day. total difficulty will be 3.
Constraints:
1 <= jobDifficulty.length <= 3000 <= jobDifficulty[i] <= 10001 <= d <= 10
Approach) Dynamic Programming (DFS)
Algorithm (Depth-first search)
- if we don't have enough jobs for the number of days return -1
- initialize the cache that will have the key to starting the index
and the number of days - the value will be the value of the max for the current job plus the
a minimum total of all days after - Depth First Search using a bottom-up approach
- We want to return the minimum total difficulty for each starting index
corresponding to each number of days left - if we have used all of our days and we have reached the end of jobs
return 0 - if we have used all our days but haven't finished all our jobs
return Infinity because we didn't complete all of our jobs (result is invalid) - create a unique key for our cache for each depth
- if the key is in the cache return the value
- calculate the last index for this day's number
- if we go beyond that index we will have more days than jobs
- the result will hold the minimum total of all following days
- max will hold the max for the current day
- iterate through the jobs updating the max and searching the remainder
- of jobs and days
- save the result in the cache and return it;
Code:
/**
* @param {number[]} jobDifficulty
* @param {number} d
* @return {number}
*/
var minDifficulty = function(jobDifficulty, d) {
// if we don't have enough jobs for the number of days return -1;
if (jobDifficulty.length < d) return -1;
// initialize the cache that will have the key of starting index
// and number of days
// the value will be the value of the max for the current job plus the
// minimum total of all days after
const cache = {};
// Depth First Search using a bottom up approach
// We want to return the minimum total difficulty for each starting index
// corresponding to each number of days left
const dfs = (start, numDays) => {
// if we have used all of our days and we have reach the end of jobs
// return 0
// if we have used all our days but haven't finished all our jobs
// return Infinity because we didn't complete all of our jobs (result is invalid)
if (numDays === d) {
return start === jobDifficulty.length ? 0 : Infinity
}
// create a unique key for our cache for each depth
const key = `${start}-${numDays}`
// if the key is in the cache return the value
if (cache[key] !== undefined) return cache[key];
// calculate the last index for this day's number
// if we go beyond that index we will have more days than jobs
const end = jobDifficulty.length - d + numDays;
// result will hold the minimum total of all following days
let result = Infinity;
// max will hold the max for the current day
let max = -Infinity
// iterate through the jobs updating the max and searching the remainder
// of jobs and days
for (let i = start; i <= end; i++) {
max = Math.max(max, jobDifficulty[i]);
result = Math.min(result, max + dfs(i + 1, numDays + 1));
}
// save the result in the cach and return it;
return cache[key] = result;
}
return dfs(0, 0);
};const minDifficulty = (A, D) => {
let n = A.length, inf = Infinity, maxd;
if (n < D) return -1;
let dp = new Array(n + 1).fill(Infinity);
dp[n] = 0;
for (let d = 1; d <= D; d++) {
for (let i = 0; i <= n - d; i++) {
maxd = 0, dp[i] = inf;
for (let j = i; j <= n - d; j++) {
maxd = Math.max(maxd, A[j]);
dp[i] = Math.min(dp[i], maxd + dp[j + 1]);
}
}
}
return dp[0];
}Input: an array of job difficulties, call it A, and a number of days, call it D.
First, let's assume that we have an array, call it DP, of size ( n + 1), where n is the length of the input array.
Loop 1: iterates from day 1 to day D, which is the amount of days given. For every iteration of this outer loop, dp[0] will contain an updated answer depending on how many days have passed. For instance, after 2 iterations, we will have the correct minimum difficulty for inputs A and D = 2 stored in dp[0]. We will start at 1 day, and work our way up to the given D days.
Now, let’s take a detailed look at what’s happening to our DP array as we go through the inner loops. Below is what happens at every iteration of d. The “===“ line indicates the end of a day.
A = [6,5,7,3]
D = 3
DAY ONE
i is: 0, j is: 0, maxd is: 6, dp array: [ Infinity, Infinity, Infinity, Infinity, 0 ]
i is: 0, j is: 1, maxd is: 6, dp array: [ Infinity, Infinity, Infinity, Infinity, 0 ]
i is: 0, j is: 2, maxd is: 7, dp array: [ Infinity, Infinity, Infinity, Infinity, 0 ]
i is: 0, j is: 3, maxd is: 7, dp array: [ 7, Infinity, Infinity, Infinity, 0 ]
(i++)
i is: 1, j is: 1, maxd is: 5, dp array: [ 7, Infinity, Infinity, Infinity, 0 ]
i is: 1, j is: 2, maxd is: 7, dp array: [ 7, Infinity, Infinity, Infinity, 0 ]
i is: 1, j is: 3, maxd is: 7, dp array: [ 7, 7, Infinity, Infinity, 0 ]
(i++)
i is: 2, j is: 2, maxd is: 7, dp array: [ 7, 7, Infinity, Infinity, 0 ]
i is: 2, j is: 3, maxd is: 7, dp array: [ 7, 7, 7, Infinity, 0 ]
(i++)
i is: 3, j is: 3, maxd is: 3, dp array: [ 7, 7, 7, 3, 0 ]
PAUSE
What does [ 7, 7, 7, 3, 0 ] mean?
Well, let’s start from the right. Forget about the 0 for a bit.
3 means that A. we have one job at A[3] that is of difficulty 3, and B. we have only one day of work.
Given these two conditions, the minimum difficulty is clearly 3. We would have to complete A[3] = 3 in one day.
Now, let’s move to the left. We have a 7. What does the 7 mean?
7 means that A. We have two jobs starting at A[2], namely [7, 3], and B. still only one day to work with (we are still on the first iteration of the outermost loop)
Given these two conditions, the minimum difficulty of our schedule is 7 because we would have to complete A[2] = 7 and A[3] = 3 on the same day.
Let's move one more to the left, what does this 7 at dp[1] mean?
It means that if A. we have three jobs starting at A[1], namely [5, 7, 3], and B. one day to work, then the minimum difficulty is 7.
We would have to complete A[1] = 5, A[2] = 7, and A[3] = 3 on the same day.
This all seems correct, but we don’t quite see how these answers are being generated.
Let’s look at what happens on day 2.
DAY TWO
i is: 0, j is: 0, maxd is: 6, dp array: [ 13, 7, 7, 3, 0 ]
PAUSE
What just happened?
maxd is the maximum difficulty that we have encountered thus far, currently located at A[0] = 6.
Now, pay very close attention to the following.
Question: If we complete job 6 on the FIRST day, and every other job on the SECOND day, what is the total minimum difficulty of our job schedule?
Two-part answer:
A. if we complete job 6 in one day, the first day's total difficulty is 6.
Ok, that’s the first day, but what is the total difficulty of all the other jobs starting from index j + 1, namely [5, 7, 3], completed on the second day?
B. We already know the answer to this question! It’s in dp[j + 1], or dp[1].
Look above! We already found that for [5, 7, 3], completing all the jobs in one day would yield a difficulty of 7.
6 + 7 = 13
At this point, the intuition behind Math.min(dp[i], maxd + dp[j + 1]) should start to become apparent, but don’t worry if not totally clear yet. Let’s do a few more iterations.
i is: 0, j is: 1, maxd is: 6, dp array: [ 13, 7, 7, 3, 0 ]
i is: 0, j is: 2 , maxd is: 7, dp array: [ 10, 7, 7, 3, 0 ]
PAUSE.
What just happened?
maxd remained 6 for one iteration, and our dp array remained exactly the same, but then maxd became 7 since j reached 2 and A[2] = 7, which is max([6,5,7]).
Now, again, pay very close attention to the following.
Question: If we complete jobs [6, 5, 7] on the first day, and all of the rest of the jobs starting at index j + 1, namely [3] on the next day (the second day), what is the total minimum difficulty of our job schedule?
Two-part answer:
A. if we complete job [6, 5, 7] in one, that day's total difficulty is 7 (or maxd!)
Ok, that’s the first day, but what is the total difficulty of all the other jobs starting at index j + 1, namely [3] completed on the second day?
B. We already know the answer to this question! It’s in dp[j + 1]. We already found, in the very beginning of our analysis, that for [3], completing all the jobs (or in this case, 1 job) in one day would yield a difficulty of 3.
7 + 3 = 10, and we just found a new minimum! If we divide the jobs like this : first day: [6, 5, 7], second day: [3], we get 10 as our minimum difficulty.
But we’re not done yet! The input has D = 3. Let’s fast forward to day 3!
(i++)
i is: 1, j is: 1, maxd is: 5 dp array: [ 10, 12, 7, 3, 0 ]
i is: 1, j is: 2, maxd is: 7, dp array: [ 10, 10, 7, 3, 0 ]
(i++)
i is: 2, j is: 2, maxd is: 7, dp array: [ 10, 10, 10, 3, 0 ]
DAY THREE
i is: 0, j is: 0, maxd is: 6, dp array: [ 16, 10, 10, 3, 0 ]
PAUSE
What just happened?
maxd = 6, which is the maximum difficulty so far (obviously, we are still at j = 0, and we haven’t passed any other difficulties)
Now, once again, pay very close attention to the following.
Question: If we complete job [6] on the first day, and all of the rest of the jobs, namely [5,7,3] this time during the next TWO days, day 2 and day 3, what will be the total minimum difficulty of our job schedule?
Two-part answer:
A. if we complete job [6] in one day, the first day's total difficulty is 6, or maxd!
Ok, that’s the first day, but what is the total difficulty of all the other jobs starting at index j + 1, namely [5, 7, 3] completed on the second AND third day.
B. We already know the answer to this question! It’s in dp[j + 1], or dp[1]. We already found, during the previous day when d = 2, i = 1, and j = 2, that for [5, 7, 3], completing all the jobs in two days would yield a difficulty of 10.
6 + 10 = 16.
i is: 0, j is: 1, maxd is: 6, dp array: [ 16, 10, 10, 3, 0 ]
(i++)
i is: 1, j is: 1, maxd is: 5, dp array: [ 16, 15, 10, 3, 0 ]
Now, let's summarize the algorithm.
- For each day, we want to update dp from i = 0 to i = n - d.
- Why n - d? Well, think of it this way. After d = 1 is completed, our dp looks like this : [ 7, 7, 7, 3, 0 ]
- When d = 2, would it make sense to update dp[3]? No, because we can't distribute one job, namely, [3] over 2 days.
- This upper limit ensures that we never update dp where there aren't enough jobs to fill the days specified by our outer loop.
- For each iteration of i over dp, we want to go over all of the elements in A from j = i to j = n - d.
- In this innermost loop, keep track of maxd, and for each iteration, the minimum is either dp[i] or maxd + dp[j + 1], whichever is smallest.
Now two final things.
- What's up with the 0 at the end of our dp array?
- We need that 0 to properly update dp during day 1.
- Why do we reassign dp[i] = inf at the beginning of each iteration of the second loop?
- If we don't assign infinity, dp[i] might not be replaced with a new value.
i + 1) and with one less day d - 1 to complete those jobs).const findMaxArr = (arr, start) => {
let max = -Infinity;
for (let i = start; i < arr.length; i++) {
max = Math.max(max, arr[i]);
};
return max;
}
const minDifficulty = (jobDifficulty, d) => {
const cache = new Map();
const findMin = (jobDifficulty, d, start) => {
if (jobDifficulty.length - start < d) return -1;
let maxToday = -Infinity;
let minTotal = Infinity;
// cache the minimum difficulty for a schedule starting at start and with d days remaining
const cachedMinimum = cache.get(`${start}#${d}`);
if (cachedMinimum) {
return cachedMinimum;
}
if (d === 1) {
const max = findMaxArr(jobDifficulty, start);
cache[`${start}-${d}`] = max;
return max;
};
for (let i = start; i < jobDifficulty.length - d + 1; i++) {
const nextMinDifficulty = findMin(jobDifficulty, d - 1, i + 1);
maxToday = Math.max(jobDifficulty[i], maxToday);
minTotal = Math.min(
minTotal,
nextMinDifficulty + maxToday,
);
};
cache.set(`${start}#${d}`, minTotal);
return minTotal;
}
return findMin(jobDifficulty, d, 0);
};
const findMaxArr = (arr, start) => {
let max = -Infinity;
for (let i = start; i < arr.length; i++) {
max = Math.max(max, arr[i]);
};
return max;
}
const minDifficulty = (jobDifficulty, d) => {
const cache = new Map();
const findMin = (jobDifficulty, d, start) => {
if (jobDifficulty.length - start < d) return -1;
let maxToday = -Infinity;
let minTotal = Infinity;
// cache the minimum difficulty for a schedule starting at start and with d days remaining
const cachedMinimum = cache.get(`${start}#${d}`);
if (cachedMinimum) {
return cachedMinimum;
}
if (d === 1) {
const max = findMaxArr(jobDifficulty, start);
cache[`${start}-${d}`] = max;
return max;
};
for (let i = start; i < jobDifficulty.length - d + 1; i++) {
const nextMinDifficulty = findMin(jobDifficulty, d - 1, i + 1);
maxToday = Math.max(jobDifficulty[i], maxToday);
minTotal = Math.min(
minTotal,
nextMinDifficulty + maxToday,
);
};
cache.set(`${start}#${d}`, minTotal);
return minTotal;
}
return findMin(jobDifficulty, d, 0);
};Conclusion
That’s all folks! In this post, we solved LeetCode problem #1335. Minimum Difficulty of a Job Schedule
I hope you have enjoyed this post. Feel free to share your thoughts on this.
You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.
In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!

Comments
Post a Comment