240. Search a 2D Matrix II

 Search a 2D Matrix II

Problem Description

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

 

Example 1:

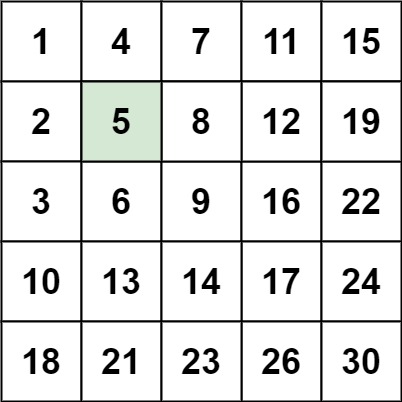
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

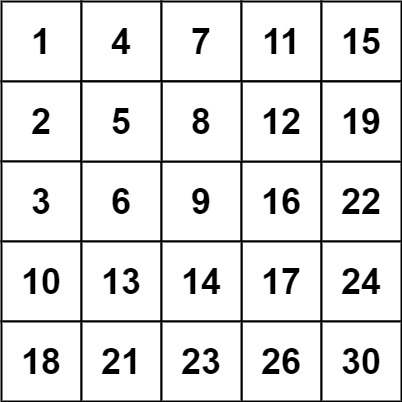
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -109 <= target <= 109

Approach) binary search

Idea:

The naive approach here would be to check every cell at a time complexity of O(m * n). The obvious improvement on this would be to use a binary search on each row to shorten this to O(m * log n). 

But since the matrix (M) is sorted both by row and by column, we can actually think of each cell (M[i][j]) as being a midpoint in a longer "row", including all the cells to the left as well as below the current cell.

If we start from the top right corner of M and treat this like a modified binary search, we can eliminate an entire row or an entire column each time we check a cell:

We'll then just need to adjust our i or j value to move to the top right corner "midpoint" of the remaining matrix each time to narrow in on our target (T):

This will drop the time complexity to O(m + n).

(Note: This works just as well when starting from the bottom left corner.)

Implementation:

For all except Java we can use the bitwise NOT operator (~) to check for boundary condition of j because it will return a falsy value (0) only when j is -1.

(Note: Some people are achieving "faster" results by exploiting a design flaw in the testing suite. It appears that the test includes one or more loops of the same matrix input and people have had the idea to clear the matrix before returning the answer, which will make the rest of said loop easier to process, as the mutated matrix will be used in subsequent iterations of the test.)

Code:

var searchMatrix = function(M, T) {
    let y = M.length, i = 0, j = M[0].length - 1
    while (i < y && ~j) {
        let cell = M[i][j]
        if (cell === T) return true
        else if (cell > T) j--
        else i++
    }
    return false
};

OR

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function(matrix, target) {
    let i = matrix.length - 1;
    let j = 0;
    while (i >= 0 && j < matrix[0].length) {
        if (matrix[i][j] > target) {
            i --;
        }
        else if (matrix[i][j] < target) {
            j ++;
        }
        else {
            return true;
        }
    }
    return false;
}

Conclusion

That’s all folks! In this post, we solved LeetCode problem #240. Search a 2D Matrix II

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!