587. Erect the Fence

Erect the Fence

Problem Description

You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.

You are asked to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed.

Return the coordinates of trees that are exactly located on the fence perimeter.

 

Example 1:

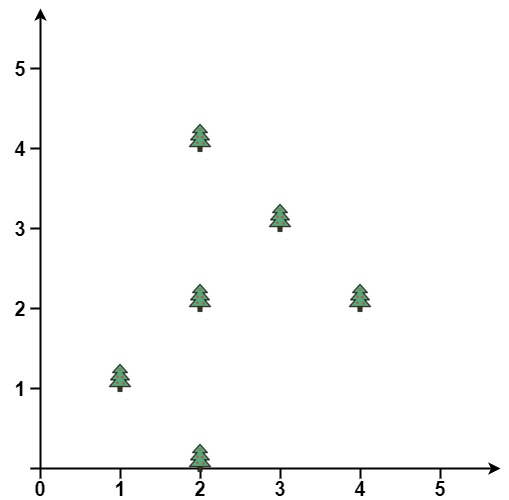
Input: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[3,3],[2,4],[4,2]]

Example 2:

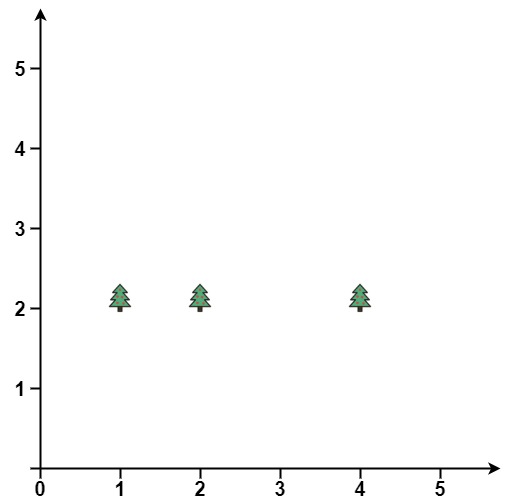
Input: points = [[1,2],[2,2],[4,2]]
Output: [[4,2],[2,2],[1,2]]

 

Constraints:

• 1 <= points.length <= 3000
• points[i].length == 2
• 0 <= xi, yi <= 100
• All the given points are unique.

Approach) Stack 

var outerTrees = function (trees) {
  trees.sort((b, a) => (a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]));

  let stack = [];

  const checkDistance = (arr, newCoor) =>
    (arr[1][1] - arr[0][1]) * (newCoor[0] - arr[1][0]) <
    (arr[1][0] - arr[0][0]) * (newCoor[1] - arr[1][1]);

  for (let each of trees) {
    while (stack.length >= 2 && checkDistance(stack.slice(-2), each))
      stack.pop();
    stack.push(each);
  }

  for (let i = trees.length - 1; i >= 0; i--) {
    while (stack.length >= 2 && checkDistance(stack.slice(-2), trees[i]))
      stack.pop();
    stack.push(trees[i]);
  }
    
  return [...new Set(stack.map(JSON.stringify))].map(JSON.parse);
};

Approach) Graham Scan

LOGIC
We look at the logic in 4 parts.

PART 0: INTUITIONS
Let's say that we have a structure as seen below.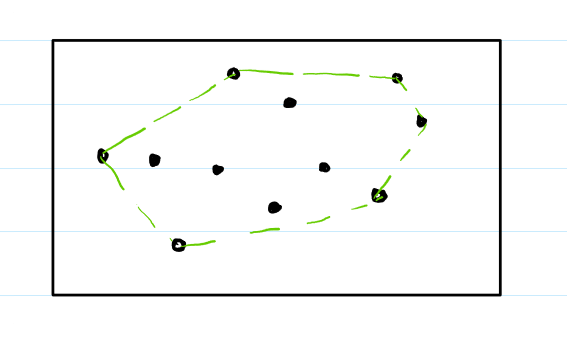

In this case, I have marked the perimeter with dotted green lines. It looks as if we have a "wrapping" of all the points inside - the "gift" with the outer path as the "wrapper".

Mathematically speaking, we are looking at a convex hull. This is different from the non-convex hull which has this one angle > 180 degrees. It is marked in red.

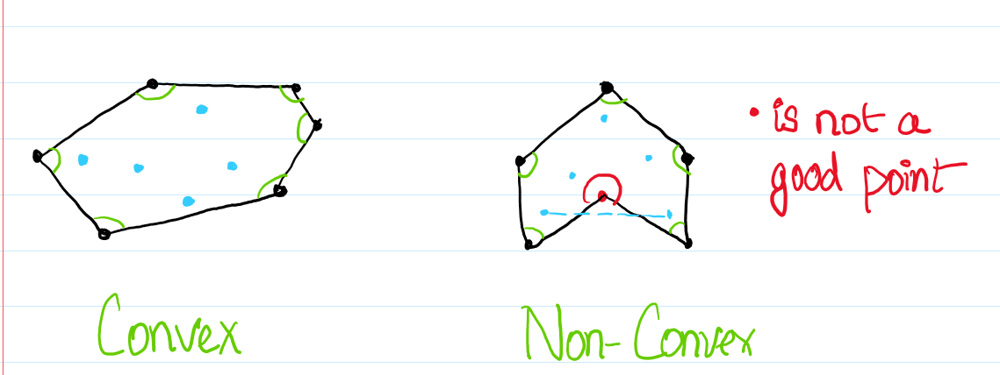
PART 1: Finding the Angle
It is clear that finding the angle is important. So, let's do that. But immediately, we are faced with a problem.

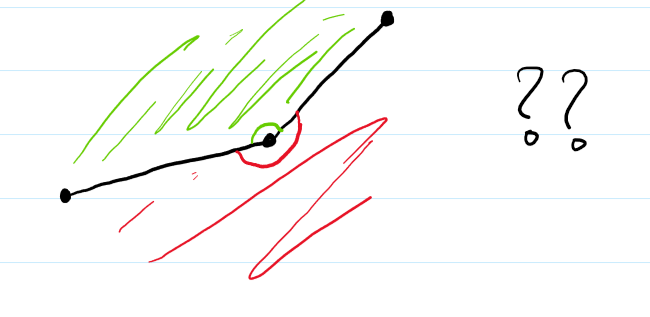
Is this green or red? We have no way of telling. So, we need to first introduce some order in the nodes. The blue arrows represent the order.

This makes it clear as to which side to select. Thus, we sort the points. This allows us to go in a clockwise direction. It's also clear that m23 > m12 holds. At this point, finding the exact angle would be a pain, so let's endure the pain of some basic algebra instead.

Note that because of sorting, we could get rid of the denominator.

PART 2: ITERATE
Now, the question is, how do we iterate over the nodes? We see that at least 3 points are required to make a judgment of two slopes. One point is the current one, and let the other two be the last one we have considered.

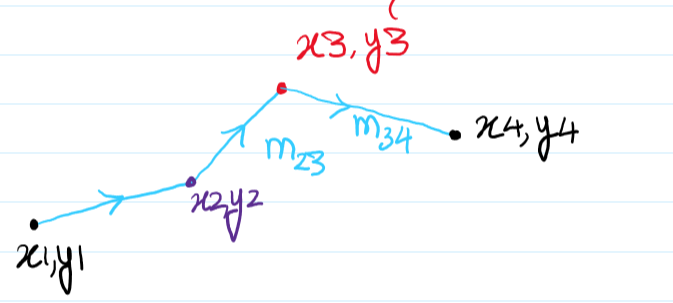
A case like the above shows that x3, y3 and x2, y2 are important, as we thought. Also, m34 < m23, which does not sound good. It makes the point x3, y3 a bad node since it is giving us the non-convex hull. So, we remove it. Easy!

Note that we may need to remove multiple "bad" points once we get a point like x4, y4. Think why.

PART 3: WHERE TO START?
There's a big flaw in the current approach. Given our assumption of going clockwise, what do we do if we have a case like below?

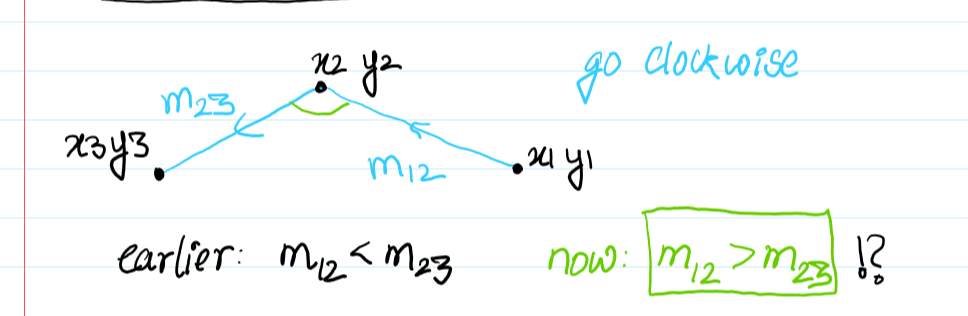
Clearly, this is also a part of the valid convex hull. The directions however have been reversed. It looks like we need to take care of the two cases:

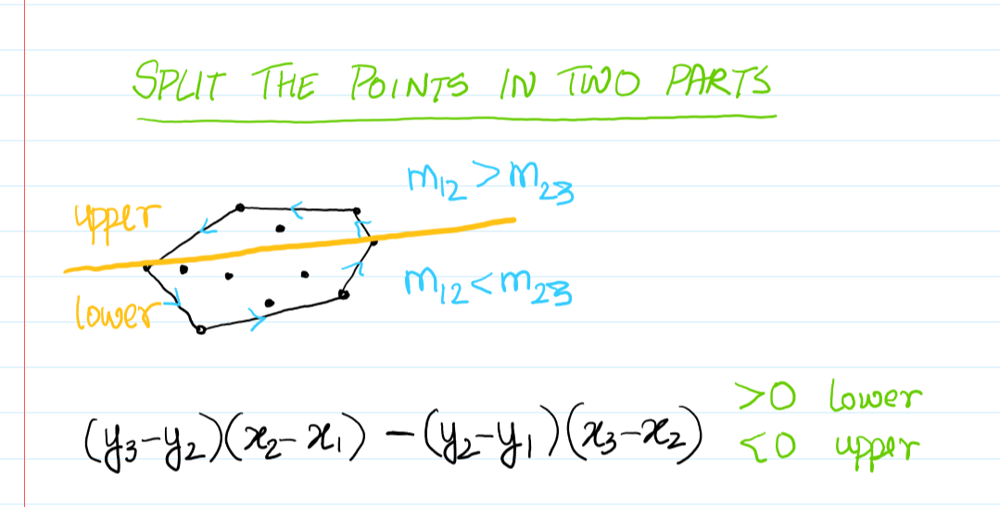
And this is it. 

const outerTrees = (trees) => {
    trees.sort((x, y) => {
        if (x[0] == y[0]) return x[1] - y[1];
        return x[0] - y[0];
    });
    let lower = [], upper = [];
    for (const tree of trees) {
        while (lower.length >= 2 && cmp(lower[lower.length - 2], lower[lower.length - 1], tree) > 0) lower.pop();
        while (upper.length >= 2 && cmp(upper[upper.length - 2], upper[upper.length - 1], tree) < 0) upper.pop();
        lower.push(tree);
        upper.push(tree);

    }
    return [...new Set(lower.concat(upper))];
};

const cmp = (p1, p2, p3) => {
    let [x1, y1] = p1;
    let [x2, y2] = p2;
    let [x3, y3] = p3;
    return (y3 - y2) * (x2 - x1) - (y2 - y1) * (x3 - x2);
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 587. Erect the Fence

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!