62. Unique Paths

Unique Paths

Problem Description

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

 

Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

 

Constraints:

• 1 <= m, n <= 100

Approach) Dynamic Programming

Essentially we have 2 base cases where we know that:

• a 1x1 grid only has 1 path possible
• if we theoretically get a grid where m or n is 0, then the grid is invalid and there are 0 possible paths.

With memoization, we can pass down a hash that keeps track of values we have already calculated. If we have already previously saved the value, then we can simply add another base case where it simply returns the value saved in our memoization hash.

If we imagine unique paths as a tree of paths, we can either move down or right. Each decision effectively shrinks the grid size by either 1 row when we go down or 1 column when we go right. When drawn out, we can clearly see duplicate nodes that would return the same values, so we can simply save the first solution and refer back to it whenever we encounter it again.
Time: O(m * n)
Space: O(m + n)

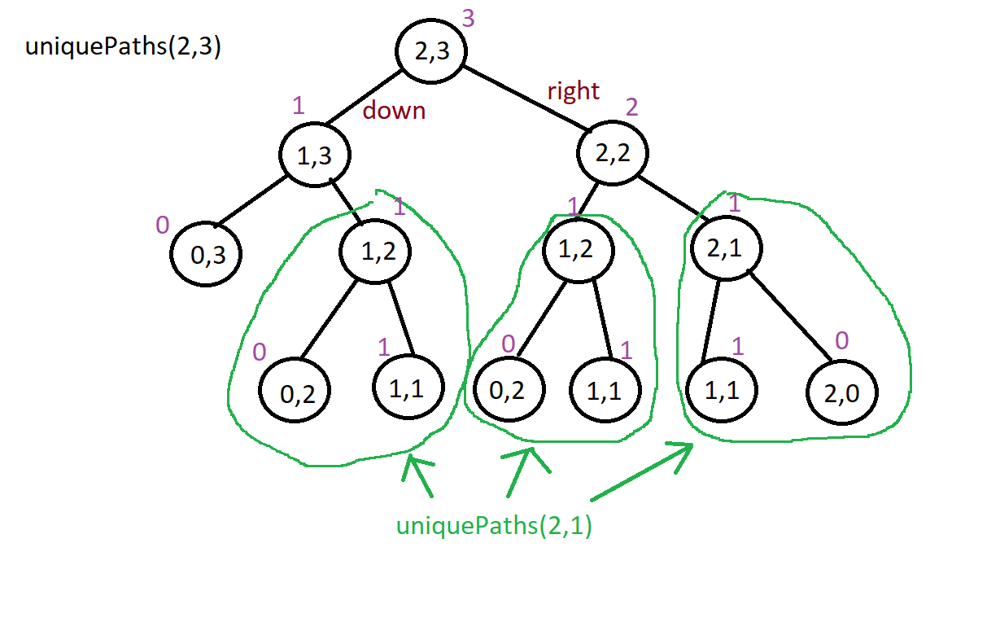
 const uniquePaths = function(m, n, memo = {}) {
     const key = m + ',' + n;
     if (key in memo) return memo[key];
     if (m === 1 || n === 1) return 1
     if (m === 0 || n === 0) return 0;
     
     memo[key] = uniquePaths(m-1, n, memo) + uniquePaths(m, n-1, memo);
     return memo[key];
};

Approach) Recursion + Memo

The number of possible paths from grid[row][col] to the bottom-right 
= the number of possible paths from grid[row][col+1] + the number of possible paths from grid[row+1][col]

1. We will use DFS to traverse every possible path starting at (0,0). The function dfs() will be called
recursively until the bottom-right (where row = height-1, col = width-1) is reached. 
- Once the bottom-right is reached, 1 is returned because it means there is a path.
- If invalid row or col index is given, 0 will be returned. 
- If given row and col have already been visited, the result will be returned from this memoization table.
- If given row and col are valid, not bottom-right, unvisited position, we will call dfs one to the right and one to the bottom, add these results, record it to our memoization table and return it.

We will use a m x n 2-d array for a memoization table.
 

var uniquePaths = function(m, n) {
    let memo = new Array(m).fill(0).map(() => new Array(n));
    return dfs(0, 0, m, n, memo);
    // T.C: O(M * N), M = # of rows, N = # of columns
    // S.C: O(M * N)
};

// Returns the number of possible paths from given (row,col) to the bottom-right
function dfs(row, col, height, width, memo) {
    // invalid index
    if (row < 0 || row >= height || col < 0 || col >= width) {
        return 0;
    }
    // the right-bottom is reached
    if (row === height-1 && col === width-1) {
        return 1;
    }
    if (memo[row][col] !== undefined) {
        return memo[row][col];
    }
    let res = dfs(row, col+1, height, width, memo) + dfs(row+1, col, height, width, memo);
    memo[row][col] = res;
    return res;
}

Approach) Combinatorics

var uniquePaths = function(m, n) {
    // This problem will solved with Combinatorics Formules in easy way!
     
     // For example: m=4, n=3;  Count of R = n-1; Count of D = m-1;
     // We can imagine this question like this => RRDDD -> we have to find all number of distinguishable permutations of 'RRDDD'
     
     // Formule ((m+n-2)!)/((m-1)! + (n-1)!);

    // Here is link to learn about Distinguishable Permutations:            https://online.stat.psu.edu/stat414/lesson/3/3.4
     
  const factarial = (n) => {
    if(n>1){return n*factarial(n-1)}
    else return 1;
  };
     
  return factarial(m+n-2)/(factarial(m-1)*factarial(n-1))
     
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 62. Unique Paths

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!