79. Word Search

Word Search

Problem Description

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

 

Example 1:

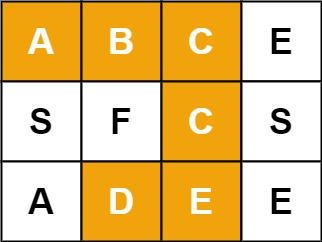
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

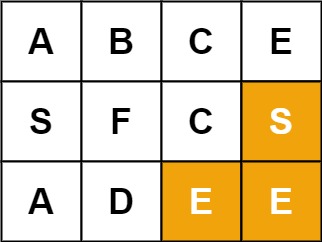
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

 

Constraints:

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board and word consists of only lowercase and uppercase English letters.

 

Follow-up: Could you use search pruning to make your solution faster with a larger board?

Approach) Recursion

Ideally, you want to look at an algorithm and come up with a technique before attempting it. In this case, it's obvious there can be almost infinite ways to make a word. Recursion is a great way to solve any algorithm when there are so many options. In the first function we loop through the board until we find a match with the first letter of the word. Once we find the first letter we use a separate Search function to traverse every possible combination(up, down, left, right) and if the function returns true we return True right away. Otherwise we keep checking until we break out of the loop and if so then there must not be a match and we return false. Remember in our Search function every time we hit a recursive call, each call will hit all 4 recursive statements.

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    for (let c = 0; c < board.length; c++) { // Our column
        for (let r = 0; r < board[c].length; r++) { //Our row
            if (board[c][r] === word[0]) { // If any letter matches the first letter of our word

                if (search(board, word, c, r)) return true; // If the search function returns true.....Return True.
				// It's worth mentioning that there will be many traversals that return false. We are only looking for at least One True statement...even if there are 100 false traversals, which is highly likely.
				//Our search function will pass in the c and r so we know the position of the letter
            }
        } 
    }
    return false; // If we made it this far the word must not be in our board.
};

const search = (b, w, c, r) => {
    if (w === "") return true; // Our basecase..If the string is empty we have found it.
    if (!(c >= 0) || !(c < b.length) || !(r >= 0) || !(r < b[c].length)) return false;  // Another basecase. If the column or row is out of bounds we must return false.
    if (b[c][r] != w[0]) return false; // Another check where if the first letter does not equal our coordinates return false

    let temp = b[c][r] //We need to mark the position as searched, and we do this with '#', because there are independent recursive calls from one another....others may need the actual letter at that position. So we put back the variable at that position after the recursive call at the bottom, so other recursive calls have it.
    b[c][r] = '#';
	// If Any of the recursive calls return True it will enter the top of the IF statement...otherwise it hits the ELSE part of the If statement. Another way to think of the recursive calls is traversal, if any traversal finds the word we return true.
    if (search(b, w.slice(1), c + 1, r) || //This is how we search Down the board
        search(b, w.slice(1), c - 1, r) || // This is how we search Up the board
        search(b, w.slice(1), c, r + 1) || // This is how we search to the Right of the board
        search(b, w.slice(1), c, r - 1)) { // This is how we search to the Left of the board
            b[c][r] = temp; // If we made it this far our recursive call has completed so put back the value on the board for any other recursive calls that may follow.
            return true; // If we made it in this part of the If statement it must be true
        } else {
            b[c][r] = temp; //Update the variable at the position for any other recursive calls that follow
            return false; // Remember our recursive calls return a boolean value. If it enters this part of the If Statement the word must not be included in our board.
        }
}

Approach) Depth First Search

var exist = function(board, word) {
  for(let r=0;r<board.length;r++){
    for(let c=0;c<board[r].length; c++){
      if(board[r][c] !== word[0]) continue
      if(dfs(board, r, c, word)) return true
    }
  }
  return false
};

function dfs(g, r, c, w, idx=0){
  if(idx === w.length) return true
  if(r<0||r>=g.length||c<0||c>=g[r].length) return false
  if(g[r][c] !== w[idx]) return  false
  if(g[r][c] === 0) return false 
  const temp = g[r][c]
  g[r][c] = 0
  const found = dfs(g, r+1, c, w, idx+1) || 
                dfs(g, r-1, c, w, idx+1) || 
                dfs(g, r, c+1, w, idx+1) ||
                dfs(g, r, c-1, w, idx+1)
  g[r][c] = temp
  return found
} 

Approach) Backtracking

var exist = function(board, word) {
  /*
    lets divide this into smaller steps
    - we need to traverse through 2d board.
    - on EVERY letter we call backtrack function.
    - backtrack function will continue calling itself as long as the conditions are valid.
    - it will return true(we have the word in the board) if we moved on the board as many times as word's length
  */
  const rows = board.length
  const cols = board[0].length
  
  const backtrack = (row, col, index) => {
    // we found the match
    if (index === word.length) return true
    
    if (row < 0 || row >= rows || col < 0 || col >= cols || // out of bounds
        // different chars in the same index, this could be visited or totally different char
        board[row][col] !== word[index])  return false
    
    const currLetter = board[row][col] // keep a copy of currentChar, we will need it.
    
    // mark visited letter on the board for upcoming recursive calls(so we don't step on them)
    board[row][col] = '-'
    
    // check the neighbors (right, left, top, bottom)
    const neighbors = backtrack(row, col + 1, index+1) || 
                      backtrack(row, col - 1, index+1) || 
                      backtrack(row - 1, col, index+1) || 
                      backtrack(row + 1, col, index+1)
    
    // revert the visited mark for upcoming iterative call so we see the correct letter.
    board[row][col] = currLetter
    
    return neighbors
  }
  
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      // from each square, check if we can build a valid word
      if (backtrack(i, j, 0)) return true
    }
  }
  return false
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 79. Word Search

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!