1339. Maximum Product of Splitted Binary Tree

Maximum Product of Splitted Binary Tree

Problem Description

Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.

Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.

Note that you need to maximize the answer before taking the mod and not after taking it.

 

Example 1:

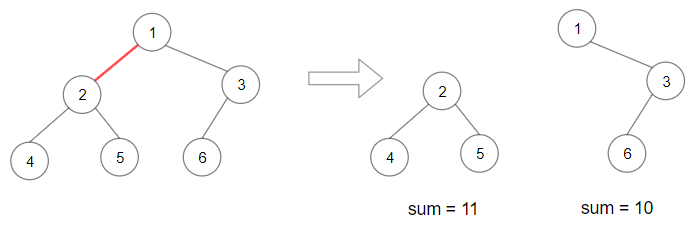
Input: root = [1,2,3,4,5,6]
Output: 110

Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

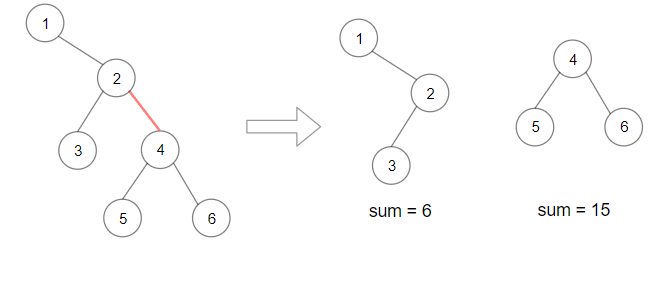
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90

Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

 

Constraints:

• The number of nodes in the tree is in the range [2, 5 * 104].
• 1 <= Node.val <= 104

Approach) Depth First Search

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxProduct = function(root) {
    let res = [];
    let MOD = Math.pow(10,9)+7;

    let dfs = function(node) {
        if (!node) return 0;
        if (!node.left && !node.right) return node.val;

        let sumL = dfs(node.left);
        let sumR = dfs(node.right);
        res.push(sumL, sumR);
        return sumL+sumR+node.val;
    }

    let totalSum = dfs(root);
    let max = 0;
    for (let e of res) {
        let cur = e * (totalSum - e);
        max = Math.max(max, cur);
    }
    return max % MOD;
};

Approach) Preorder Recursion

Recursively get the sums of each subtree. Save each sum in an array. The order does not matter. Then get the largest product of each sum and (total-sum).

Overflow Concerns - The problem calls for obtaining the largest pre-modulo product. This is where you can see how carefully the constraints were chosen. The worst-case scenario is a tree with 50000 nodes, each with a value of 10000.

The largest pre-modulo product is (10000*25000)^2 = 6.25×10¹⁶
Number.MAX_SAFE_INTEGER is roughly 9×10¹⁶

Pretty damned close, but Number will still suffice.

Complexity

• Time complexity: O(n)
• Space complexity: O(n)

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxProduct = function(root) 
{
    const MOD = 1e9+7;
    let edgeSums = [];

    const dfs = function(node)
    {
        if(!node)
            return 0;
        let sum = node.val;
        sum += dfs(node.left);
        sum += dfs(node.right);

        edgeSums.push(sum);
        return sum;
    };

    let total = dfs(root);

    let maxProd = edgeSums.reduce((acc,val)=>Math.max(acc, val*(total-val)));
    return maxProd % MOD;
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 1339. Maximum Product of Splitted Binary Tree

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!