931. Minimum Falling Path Sum

 Minimum Falling Path Sum

Problem Description

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

 

Example 1:

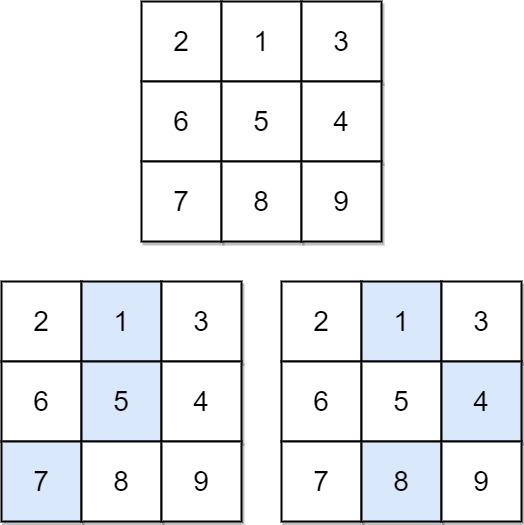
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13

Explanation: There are two falling paths with a minimum sum as shown.

Example 2:

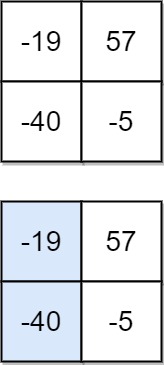
Input: matrix = [[-19,57],[-40,-5]]
Output: -59

Explanation: The falling path with a minimum sum is shown.

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

Approach) Recursion

var minFallingPathSum = function(matrix) {
    let n = matrix.length;
    let m = matrix[0].length;
    let min = Infinity;
    
    // base case - when i will be 0, dp[0][j] will be matrix[0][j]
    for(let j = 0; j < m; j++) matrix[0][j] = matrix[0][j]
    
    for(let j = 0 ; j < m; j++) {
        min = Math.min(min, compute(n - 1, j, matrix));  
    }
    return min;
};

function compute(i, j, matrix) {
    if(j < 0 || j >= matrix.length) return 10000; // big enough number
    
    if(i === 0) return matrix[0][j];
    
    let up = matrix[i][j] + compute(i - 1, j, matrix);
    let upLeft = matrix[i][j] + compute(i - 1, j - 1, matrix);
    let upRight = matrix[i][j] + compute(i - 1, j + 1, matrix);
    
    return Math.min(up, upLeft, upRight);
}

Recursion + Dynamic Programming

T.C - O(N * M) * M
S.C - O(N * M) * M

var minFallingPathSum = function(matrix) {
    let n = matrix.length;
    let m = matrix[0].length;
    let min = Infinity;
    let dp = new Array(n).fill(-1).map(() => new Array(m).fill(-1));
    
    // base case - when i will be 0, dp[0][j] will be matrix[0][j]
    for(let j = 0; j < m; j++) matrix[0][j] = matrix[0][j]
    
    for(let j = 0 ; j < m; j++) {
        min = Math.min(min, compute(n - 1, j, matrix, dp));  
    }
    
    return min;
};

function compute(i, j, matrix, dp) {
    if(j < 0 || j >= matrix.length) return 10000; // big enough number
    
    if(i === 0) return matrix[0][j];
    
    if(dp[i][j] !== -1) return dp[i][j];
    
    let up = matrix[i][j] + compute(i - 1, j, matrix, dp);
    let upLeft = matrix[i][j] + compute(i - 1, j - 1, matrix, dp);
    let upRight = matrix[i][j] + compute(i - 1, j + 1, matrix, dp);
    
    return dp[i][j] = Math.min(up, upLeft, upRight);
}

Dynamic Programming + Tabulation

T.C - O(N * M)
S.C - O(N * M)

var minFallingPathSum = function(matrix) {
    let n = matrix.length;
    let m = matrix[0].length;
    let dp = new Array(n).fill(0).map(() => new Array(m).fill(0));
    
    // tabulation // bottom-up approach
    
    // base case - when i will be 0, dp[0][j] will be matrix[0][j]
    for(let j = 0; j < m; j++) dp[0][j] = matrix[0][j]
    
    for(let i = 1; i < n; i++) {
        for(let j = 0 ; j < m; j++) {
            let up = matrix[i][j] + dp[i - 1][j];
            
            let upLeft = matrix[i][j];
            if((j - 1) >= 0) upLeft += dp[i - 1][j - 1]; // if not out of bound
            else upLeft += 10000; // big enough number
            
            let upRight = matrix[i][j];
            if((j + 1) < m) upRight += dp[i - 1][j + 1]; // if not out of bound
            else upRight += 10000; // big enough number
            
            dp[i][j] = Math.min(up, upLeft, upRight);
        }
    }
    return Math.min(...dp[n - 1]);
};

Dynamic Programming + Tabulation (Space optimized)

How it is space optimized?
In this our up left, upRight, and up value only depends on the previous row
Notice we reach the next row after the previous row right?
So why not just use the previous row to compute the next value instead of creating a 2D DP Array

var minFallingPathSum = function(matrix) {
    let n = matrix.length;
    let m = matrix[0].length;
    let prev = new Array(m).fill(0);
    let curr = new Array(m).fill(0);
    
    // tabulation // bottom-up approach
    
    // base case - when i will be 0, dp[0][j] will be matrix[0][j]
    for(let j = 0; j < m; j++) prev[j] = matrix[0][j]; 
    
    for(let i = 1; i < n; i++) {
        for(let j = 0 ; j < m; j++) {
            let up = matrix[i][j] + prev[j];
            
            let upLeft = matrix[i][j];
            if((j - 1) >= 0) upLeft += prev[j - 1]; if not out of bound
            else upLeft += 10000; // big enough number
            
            let upRight = matrix[i][j];
            if((j + 1) < m) upRight += prev[j + 1]; // if not out of bound
            else upRight += 10000; // big enough number
            
            curr[j] = Math.min(up, upLeft, upRight);
        }
        prev = curr;
    }
    return Math.min(...prev);
};

Tabulation

T.C - O(N * M)
S.C - O(1)

const minFallingPathSum = function(matrix) {
    let m = matrix.length;
    let n = matrix[0].length;
    
    for (let i = 1; i < m; i++) {
        for (let j = 0; j < n; j++) {
            matrix[i][j] = matrix[i][j] + Math.min(matrix[i - 1][j], matrix[i - 1][j - 1] || 10000, matrix[i - 1][j + 1] || 10000);
        }
    }
    return Math.min(...matrix[m - 1]);
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 931. Minimum Falling Path Sum

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!