2136. Earliest Possible Day of Full Bloom

Earliest Possible Day of Full Bloom

Problem Description

You have n flower seeds. Every seed must be planted first before it can begin to grow, then bloom. Planting a seed takes time and so does the growth of a seed. You are given two 0-indexed integer arrays plantTime and growTime, of length n each:

• plantTime[i] is the number of full days it takes you to plant the ith seed. Every day, you can work on planting exactly one seed. You do not have to work on planting the same seed on consecutive days, but the planting of a seed is not complete until you have worked plantTime[i] days on planting it in total.
• growTime[i] is the number of full days it takes the ith seed to grow after being completely planted. After the last day of its growth, the flower blooms and stays bloomed forever.

From the beginning of day 0, you can plant the seeds in any order.

Return on the earliest possible day when all seeds are blooming.

 

Example 1:

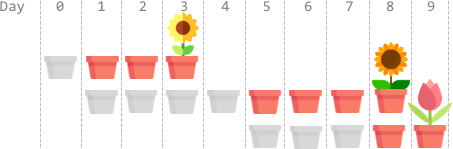
Input: plantTime = [1,4,3], growTime = [2,3,1]
Output: 9

Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 0, plant the 0th seed. The seed grows for 2 full days and blooms on day 3.
On days 1, 2, 3, and 4, plant the 1st seed. The seed grows for 3 full days and blooms on day 8.
On days 5, 6, and 7, plant the 2nd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 2:

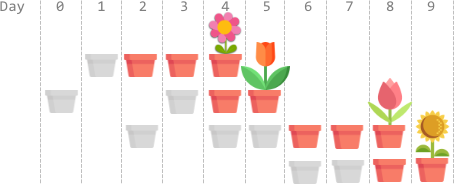
Input: plantTime = [1,2,3,2], growTime = [2,1,2,1]
Output: 9

Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 1, plant the 0th seed. The seed grows for 2 full days and blooms on day 4.
On days 0 and 3, plant the 1st seed. The seed grows for 1 full day and blooms on day 5.
On days 2, 4, and 5, plant the 2nd seed. The seed grows for 2 full days and blooms on day 8.
On days 6 and 7, plant the 3rd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 3:

Input: plantTime = [1], growTime = [1]
Output: 2

Explanation: On day 0, plant the 0th seed. The seed grows for 1 full day and blooms on day 2.
Thus, on day 2, all the seeds are blooming.

 

Constraints:

• n == plantTime.length == growTime.length
• 1 <= n <= 105
• 1 <= plantTime[i], growTime[i] <= 104

Approach) Greedy

/**
 * @param {number[]} plantTime
 * @param {number[]} growTime
 * @return {number}
 */
var earliestFullBloom = function (plantTime, growTime) {
  const array = [];
  const n = plantTime.length;

  for (let i = 0; i < n; i++) {
    array.push([plantTime[i], growTime[i]]);
  }
  array.sort((a, b) => b[1] - a[1]);

  let ans = -Infinity;
  let totalPlantTime = 0;
  for (const [plant, grow] of array) {
    totalPlantTime += plant;
    ans = Math.max(ans, totalPlantTime + grow);
  }

  return ans;
};

Approach) Another

/**
 * @param {number[]} plantTime
 * @param {number[]} growTime
 * @return {number}
 */
const earliestFullBloom = function(plantTime, growTime) {
  const sum = arr => arr.reduce((ac, e) => ac +e, 0)
  let l = 0, r = sum(plantTime) + sum(growTime)
  const n = plantTime.length

  const a = []
  for(let i = 0; i < n; i++) {
    a.push([growTime[i], plantTime[i] ])
  }

  a.sort((a, b) => a[0] === b[0] ? a[1] - b[1] : a[0] - b[0])
  a.reverse()
  function chk(d) {
    let total = -1
    let max_num = 0
    for(let i = 0; i < n; i++) {
      total += a[i][1]
      max_num = Math.max(max_num, total + a[i][0] + 1)
    }
    return max_num <= d
  }

  while (l < r) {
    let m = ~~((l + r) / 2)
    if (chk(m)) r = m
    else l = m + 1          
  }

  return l
};

Approach) Native

var earliestFullBloom = function(plantTime, growTime) {
    let mappedPlantTimeGrowTime = []
    // mapped plantTime and growTime togother to be able to sort them based on growTime
    for (let i = 0; i < growTime.length; i++) {
        mappedPlantTimeGrowTime[i] = [plantTime[i], growTime[i]]
    }
    
    // sort the array based on the growTime in decreasing order
    mappedPlantTimeGrowTime.sort((a, b) => b[1] - a[1])
    
    let sumOfPlanTime = 0, sumOfGrowTime = 0, earlistGrowTime = 0
    
    for (let i = 0; i < mappedPlantTimeGrowTime.length; i++) {
        sumOfPlanTime += mappedPlantTimeGrowTime[i][0]
        sumOfGrowTime = sumOfPlanTime + mappedPlantTimeGrowTime[i][1]
        earlistGrowTime = Math.max(earlistGrowTime, sumOfGrowTime)
    }
    return earlistGrowTime
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem #2136. Earliest Possible Day of Full Bloom

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!