1578. Minimum Time to Make Rope Colorful

Minimum Time to Make Rope Colorful

Problem Description

Alice has n balloons arranged on a rope. You are given a 0-indexed string colors where colors[i] is the color of the ith balloon.

Alice wants the rope to be colorful. She does not want two consecutive balloons to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it colorful. You are given a 0-indexed integer array neededTime where neededTime[i] is the time (in seconds) that Bob needs to remove the ith balloon from the rope.

Return the minimum time Bob needs to make the rope colorful.

 

Example 1:

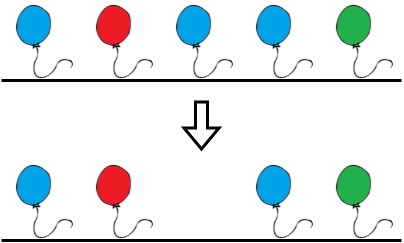
Input: colors = "abaac", neededTime = [1,2,3,4,5]
Output: 3

Explanation: In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.

Example 2:

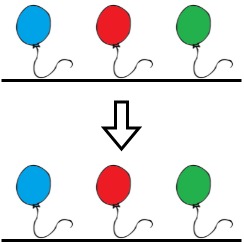
Input: colors = "abc", neededTime = [1,2,3]
Output: 0

Explanation: The rope is already colorful. Bob does not need to remove any balloons from the rope.

Example 3:

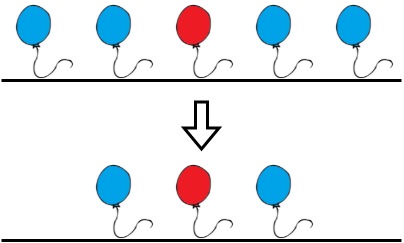
Input: colors = "aabaa", neededTime = [1,2,3,4,1]
Output: 2

Explanation: Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.

 

Constraints:

• n == colors.length == neededTime.length
• 1 <= n <= 105
• 1 <= neededTime[i] <= 104
• colors contains only lowercase English letters.

Idea:

Every time you encounter two consecutive identical ones, add ans to the smaller one of the two costs, and then update the cost to the one with the larger cost,
because for example.
when there are three repeated traversals to the second one The cost will use the smaller one, so when traversing to the third one, the cost can only be selected from the larger one and the third cost

Code:

/**
 * @param {string} colors
 * @param {number[]} neededTime
 * @return {number}
 */
var minCost = function(colors, neededTime) {
    let ans = 0;
    for(let i=1; i<colors.length; i++){
        if(colors.charAt(i)==colors.charAt(i-1)){
            ans += Math.min(neededTime[i], neededTime[i-1]);
            neededTime[i] = Math.max(neededTime[i], neededTime[i-1]);
        }
    }
    return ans;
};

OR

/**
 * @param {string} colors
 * @param {number[]} neededTime
 * @return {number}
 */
var minCost = function(colors, neededTime) {
    if (colors.length==0) { return 0; }
    let prev = colors.charAt(0);
    let ans = 0;
    for (let i=1; i<neededTime.length; i++) { 
        if (colors.charAt(i)==prev) { 
            let curr = Math.min(neededTime[i], neededTime[i-1]); 
            ans+=curr; 
            neededTime[i] = Math.max(neededTime[i], neededTime[i-1]); 
        } else { 
            prev = colors.charAt(i); 
        } 
    } 
    return ans;
};

OR

/**
 * @param {string} colors
 * @param {number[]} neededTime
 * @return {number}
 */
var minCost = function(colors, neededTime) {
   let result=0;
    let last=0;
    for(let i=1;i<colors.length;i++){
        if(colors[i]==colors[last]){
            if(neededTime[i]>=neededTime[last]){
                result+=neededTime[last];
                last=i;
            }
            else{
                result+=neededTime[i];
            }
        }
        else{
            last=i;
        }
    } 
    return result;
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem #1578. Minimum Time to Make Rope Colorful

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!