223. Rectangle Area

Rectangle Area

Problem Description

Given the coordinates of two rectilinear rectangles in a 2D plane, return the total area covered by the two rectangles.

The first rectangle is defined by its bottom-left corner (ax1, ay1) and its top-right corner (ax2, ay2).

The second rectangle is defined by its bottom-left corner (bx1, by1) and its top-right corner (bx2, by2).

 

Example 1:

Input: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
Output: 45

Example 2:

Input: ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
Output: 16

 

Constraints:

• -104 <= ax1 <= ax2 <= 104
• -104 <= ay1 <= ay2 <= 104
• -104 <= bx1 <= bx2 <= 104
• -104 <= by1 <= by2 <= 104

Approach) Math - Intuition

If the rectangles do not overlap, then the answer is obvious: add the areas of both. If they do overlap, then we are adding the overlapping part twice. In that case, we could find out the relative configuration of both rectangles, break the common figure into smaller rectangles accordingly, and then add the smaller parts together. However, there are multiple configurations, and each one would have to be treated differently: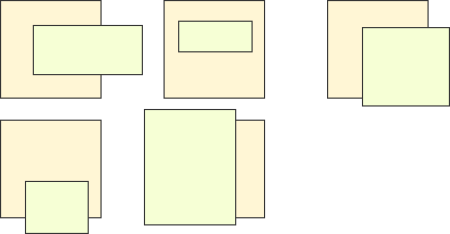







A better solution would be to add the two rectangles and simply substract the common part that was added twice:

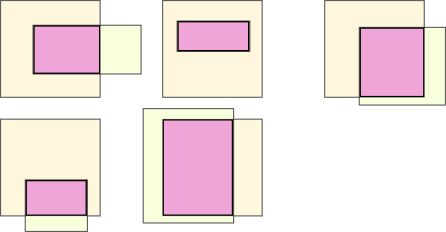
It is always a rectangle limited by the rightmost left line, the higher bottom, the leftmost right and the lower top.


Solution:
This can be solved in one line but it would be a very hacky solution that would paint a poor image in an interview ("the candidate shows little regard for readability/maintainability"). On the other hand, we could do the opposite:

/**
 * @param {number} ax1
 * @param {number} ay1
 * @param {number} ax2
 * @param {number} ay2
 * @param {number} bx1
 * @param {number} by1
 * @param {number} bx2
 * @param {number} by2
 * @return {number}
 */
var computeArea = function(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2) {
    let first  = area(ax1, ay1, ax2, ay2);
    let second = area(bx1, by1, bx2, by2);

    let leftOverlap  = Math.max(ax1, bx1);
    let downOverlap  = Math.max(ay1, by1);

    let rightOverlap = Math.min(ax2, bx2);
    let upOverlap    = Math.min(ay2, by2);

    let overlap = area(leftOverlap, downOverlap, rightOverlap, upOverlap);

    return first + second - overlap;
};

// Returns 0 if right < left or up < down
function area(left, down, right, up) {
        
    if (left > right || down > up) {
        return 0;
    }

    return (right - left) * (up - down);
    
}

Approach) Math

The intuition is to use a mathematical pattern:
the total area of two intersecting shapes = the area of each shape - the area of their intersection

The steps to solve this would be to realize this pattern and then to find the intersecting area.

It can seem confusing given the intersection could be a superset of one shape, a superset of both shapes, a subset of both shapes, or simply non-existant. I recommend drawing out examples and thinking about each scenario. I ended up with the following code:

var computeArea = function(A, B, C, D, E, F, G, H) {
    const intersectingWidth = Math.max(Math.min(C, G) - Math.max(A, E), 0)
    const intersectingHeight = Math.max(Math.min(D, H) - Math.max(B, F), 0)
    
    const intersectingArea = intersectingWidth * intersectingHeight
    
    const area1 = (C-A) * (D-B)
    const area2 = (G-E) * (H-F)
    
    return area1 + area2 - intersectingArea
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 223. Rectangle Area

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!