124. Binary Tree Maximum Path Sum

Binary Tree Maximum Path Sum

Problem Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

 

Example 1:

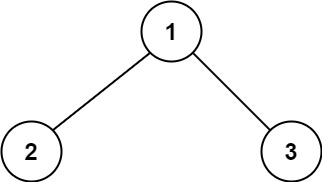
Input: root = [1,2,3]
Output: 6

Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

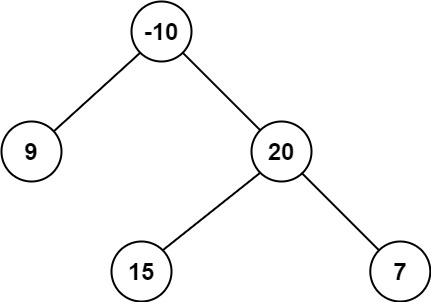
Input: root = [-10,9,20,null,null,15,7]
Output: 42

Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

 

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -1000 <= Node.val <= 1000

Approach) Depth First Search 

It's important to point out that we are looking for the maximum path. In the most simple case, a single node can be the max path, or even the entire tree could be the max path. To keep the max variable up to date, I create a global variable that will be updated over the run of the functions.

We are doing a DFS recursive function here.

We need a base case, and that base case is if we hit a null, we return 0. We are going to finish the left subtree before going to the right subtree, which is denoted by findSums(node.left) then after is findSums(node.right). After the left and right subtree are done (for an example, look at a single node), we have three different sums. All three nodes (left, right and node.val), left side (node.val and left), right side (node.val and right) or just the single node. We use these values (with the current max) to find the max.

The most important part is what do we return for this recursive function? The answer is we are returning

The Max Path from this node

That can be node.val, leftNodeSum, or rightNodeSum. We cannot return allSum since that would not be a path. Very, very important to point that out.

const maxPathSum = (root) => {
	let max = -Infinity;

	const findSums = (node) => {
		// Base case / hit a null
		if (!node) return 0;

		let left = findSums(node.left),
			right = findSums(node.right),
			allSum = left + right + node.val,
			leftNodeSum = left + node.val,
			rightNodeSum = right + node.val;

		// Max is all possible combinations
		max = Math.max(max, node.val, allSum, leftNodeSum, rightNodeSum);
		
		// Return the MAX path, which can be node.val, left + node.val, or right + node.val
		return Math.max(leftNodeSum, rightNodeSum, node.val);
	};

	findSums(root);

	return max;
};

Approach) Recursion

var maxPathSum = function(root) {
  var max = -Number.MAX_VALUE;
  getMaxSum(root);
  return max;
  function getMaxSum(node) {
    if (!node) return 0;
    var leftSum = getMaxSum(node.left);
    var rightSum = getMaxSum(node.right);
    max = Math.max(max, node.val + leftSum + rightSum);
    return Math.max(0, node.val + leftSum, node.val + rightSum);
  }
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem 124. Binary Tree Maximum Path Sum

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!