160. Intersection of Two Linked Lists

 

The intersection of Two Linked Lists

Problem Description

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at the node c1:

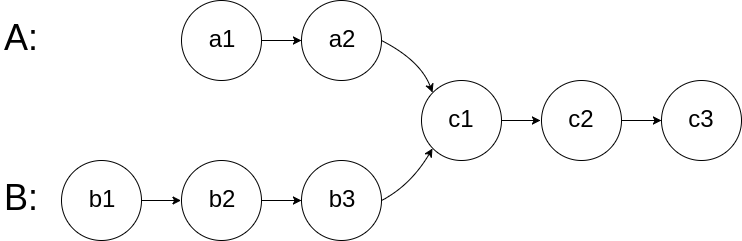
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

• intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
• listA - The first linked list.
• listB - The second linked list.
• skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
• skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.

The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.

 

Example 1:

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.

Example 2:

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

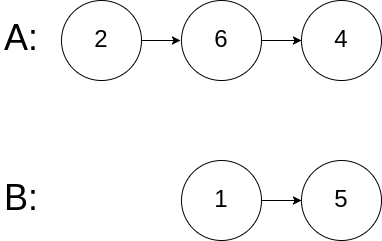
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

 

Constraints:

• The number of nodes of listA is in the m.
• The number of nodes of listB is in the n.
• 1 <= m, n <= 3 * 104
• 1 <= Node.val <= 105
• 0 <= skipA < m
• 0 <= skipB < n
• intersectVal is 0 if listA and listB do not intersect.
• intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

 

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

Idea:

The naive approach here would be to store each node reference in a data structure until we saw the same one twice, but that would take O(N) extra space.

In order to solve this problem with only O(1) extra space, we'll need to find another way to align the two linked lists. More importantly, we need to find a way to line up the ends of the two lists. And the easiest way to do that is to concatenate them in opposite orders, A+B and B+A. This way, the ends of the two original lists will align on the second half of each merged list.

Then we just need to check if at some point the two merged lists are pointing to the same node. In fact, even if the two merged lists don't intersect, the value of a and b will be the same (null) when we come to the end of the merged lists, so we can use that as our exit condition.

We just need to make sure to string headB onto a and vice versa if one (but not both) list ends.

Let`s Code IT!

var getIntersectionNode = function(headA, headB) {
    if(headA===null || headB===null) {
        return null;
    }
    
    let currA = headA;
    let currB = headB;
    while (currA !== currB) {
        currA = currA.next
        currB = currB.next
        if(currA === currB) {
            return currA;
        }
        if(currA === null) {
            currA = headB            
        }
        if(currB === null) {
            currB = headA
        }
    }
    return currA
};

We can write it In another way also as below:

var getIntersectionNode = function(headA, headB) {
    let a = headA, b = headB
    while (a !== b) {
        a = !a ? headB : a.next
        b = !b ? headA : b.next
    }
    return a
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem #160. Intersection of Two Linked Lists

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to solve leetcode questions & present the most important points to consider when improving Data structure and logic,  feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!