1926. Nearest Exit from Entrance in Maze

Nearest Exit from Entrance in Maze

Problem Description

You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.

Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

 

Example 1:

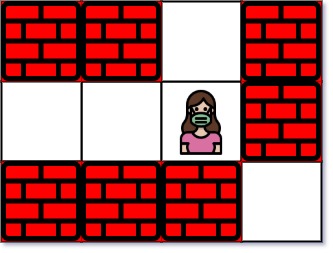
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1

Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.

Example 2:

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.

Example 3:

Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.

 

Constraints:

• maze.length == m
• maze[i].length == n
• 1 <= m, n <= 100
• maze[i][j] is either '.' or '+'.
• entrance.length == 2
• 0 <= entrancerow < m
• 0 <= entrancecol < n
• entrance will always be an empty cell.

Approach) BFS ( Breadth First Search )

/**
 * @param {character[][]} maze
 * @param {number[]} entrance
 * @return {number}
 */
const dx = [1, -1, 0, 0], dy = [0, 0, 1, -1];
const nearestExit = (g, entrance) => {
    let [n, m, ex, ey] = [g.length, g[0].length, entrance[0], entrance[1]];
    let dis = initialize2DArrayNew(n, m);
    let q = [];
    for (let i = 0; i < n; i++) { // find all exits
        for (let j = 0; j < m; j++) {
            if ((i == ex && j == ey) || g[i][j] == '+') continue;
            if (i == 0 || i == n - 1 || j == 0 || j == m - 1) {
                q.push([i, j]);
                dis[i][j] = 0; // reset to 0 for calculating the min path
            }
        }
    }
    while (q.length) { // bfs
        let cur = q.shift();
        let [x, y] = cur;
        for (let k = 0; k < 4; k++) {
            let xx = x + dx[k];
            let yy = y + dy[k];
            if (xx < 0 || xx >= n || yy < 0 || yy >= m || g[xx][yy] == '+') continue; // out of bound or wall
            if (dis[xx][yy] > dis[x][y] + 1) { // update min path
                dis[xx][yy] = dis[x][y] + 1;
                q.push([xx, yy]);
            }
        }
    }
    let res = dis[ex][ey];
    return res == Number.MAX_SAFE_INTEGER ? -1 : res;
};

const initialize2DArrayNew = (n, m) => { 
    let data = []; 
    for (let i = 0; i < n; i++) { 
        let tmp = Array(m).fill(Number.MAX_SAFE_INTEGER); 
        data.push(tmp); 
    } 
    return data; 
};

Conclusion

That’s all folks! In this post, we solved The LeetCode problem 1926. Nearest Exit from the Entrance in Maze

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!