835. Image Overlap

Image Overlap

Problem Description

You are given two images, img1 and img2, represented as binary, square matrices of size n x n. A binary matrix has only 0s and 1s as values.

We translate one image however we choose by sliding all the 1 bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the overlap by counting the number of positions that have a 1 in both images.

Note also that a translation does not include any kind of rotation. Any 1 bits that are translated outside of the matrix borders are erased.

Return the largest possible overlap.

 

Example 1:

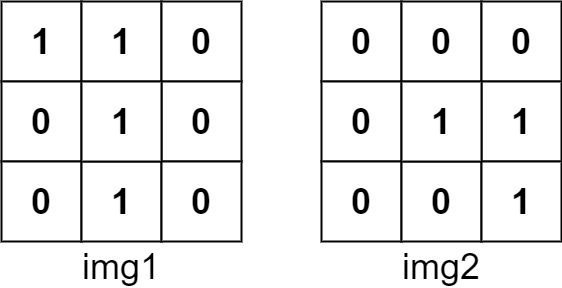
Input: img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
Output: 3

Explanation: We translate img1 to right by 1 unit and down by 1 unit.



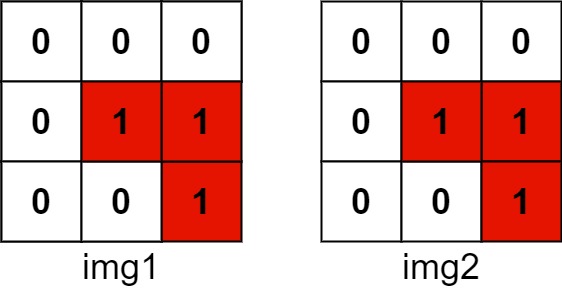
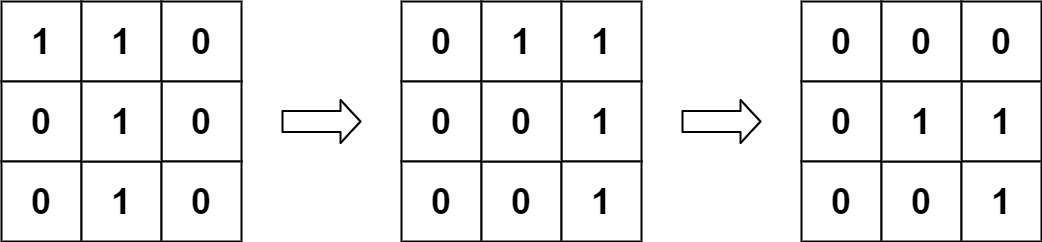The number of positions that have a 1 in both images is 3 (shown in red).

Example 2:

Input: img1 = [[1]], img2 = [[1]]
Output: 1

Example 3:

Input: img1 = [[0]], img2 = [[0]]
Output: 0

 

Constraints:

• n == img1.length == img1[i].length
• n == img2.length == img2[i].length
• 1 <= n <= 30
• img1[i][j] is either 0 or 1.
• img2[i][j] is either 0 or 1.

Approach) Brute Force

var largestOverlap = function(A, B) {
    let n = A.length;
    let max = 0;
    for (let i = -n + 1; i < n; i++) {
        for (let j = -n + 1; j < n; j++) {
            let t = 0;
            for (let x = 0; x < n; x++) {
                for (let y = 0; y < n; y++) {
                    if (x + i >= 0 && x + i < n && y + j >= 0 && y + j < n && A[x][y] === 1 && B[x + i][y + j] === 1) {
                        t++;
                    }
                }
            }
            max = Math.max(max, t);
        }
    }
    return max;
};

Approach) Linear Transformation

/*
Linear Transformation:
find cells with ones. to move a 1 from A to a 1 from B, it'll take some transformation  (dx, dy).  
for another 1 cell in A to also overlap with a 1 cell in B will take the SAME (dx,dy). 
make a map of possible (dx,dy) and count the ones that have the same (dx,dy)

find [[i,j]...] of 1s for A, B
find all combos of each filtered array
calc the dx,dy and set to a map.  find the mapping that has the highest count and return

T: filtering takes O(N^2). combos takes a double for loop of N^2 * N^2 in the worst case. 
so N^2 + N^2 * N^2 ---> O(N^4)
S: O(N^2) for arrays space in the worst case of A and B filled with 1s
*/
var largestOverlap = function(A, B) {
    let overlaps = 0;
    let aArr = [];
    let bArr = [];
    for (let i = 0; i < A.length; i++){
        for (let j = 0; j < A[0].length; j++){ // find 1s
            if (A[i][j] === 1) aArr.push([i,j]);
            if (B[i][j] === 1) bArr.push([i,j]);
        }
    }
    let map = new Map(); // {dx#dy : count}
    for (const coordA of aArr){
        for (const coordB of bArr){
            let dx = coordB[0] - coordA[0];
            let dy = coordB[1] - coordA[1];
            let key = dx + "#" + dy;
            map.set(key, (map.get(key) || 0) + 1);
            overlaps = Math.max(overlaps, map.get(key));
        }
    }
    return overlaps;
}

Approach) Better Brute Force

The point is that every position in B can be moved to position A And we just move it to see why kind of move is needed and then aggregate by move! genius

/**
 * @param {number[][]} A
 * @param {number[][]} B
 * @return {number}
 */
var largestOverlap = function(A, B) {
    // prepare
    const listA = [];
	const listB = [];
    for ( let i = 0 ; i < A.length ; i++ ) {
        for ( let j = 0 ; j < A[0].length ; j++ ) {
            if ( A[i][j] ) listA.push([i, j]);
			if ( B[i][j] ) listB.push([i, j]);
        }
    }
    
    // the point is that every position in B can be moved to position A
    // And we just move it to see why kind of move is needed
    // and then aggregate by move ! genius
    const cache = {};
    let max = 0;
    for ( let i = 0 ; i < listA.length ; i++ ) {
        for ( let j = 0 ; j < listB.length ; j++ ) {
            const str = `${listA[i][0]-listB[j][0]}_${listA[i][1]-listB[j][1]}`;
            cache[str] = cache[str] || 0;
            cache[str] += 1;
            max = Math.max( max, cache[str] );
        }
    }
    
    return max;
};

Approach) Using Find, Map, and Filter

const helper = (pos, x, y, n) => {
    return pos.map(([l,r]) => [l+x, r+y])
        .filter(([l,r]) => l < n && r < n && l >= 0 && r >= 0);
}

const getOverlap = (pos1, pos2) => {
    let overlap = 0;
    
    for(let [l,r] of pos1) {
        if(pos2.find(el => el[0] === l && el[1] === r)) overlap++;
    }
    
    return overlap;
}

const largestOverlap = function(img1, img2) {
    const n = img1.length;
    const [pos1, pos2] = [[],[]];
    for(let i = 0; i < n; i++) {
        for(let j = 0; j < n; j++) {
            if(img1[i][j] === 1) {
                pos1.push([i,j])
            }
            if(img2[i][j] === 1) {
                pos2.push([i,j])
            }
        }
    }
    let max = 0;
    for(let i = 1-n; i < n; i++) {
        for(let j = 1-n; j < n; j++) {
            const temp1 = helper(pos1,i,j,n);
            const temp2 = helper(pos2,i,j,n);
            max = Math.max(max,getOverlap(temp1, pos2));
            max = Math.max(max,getOverlap(temp2, pos1));
        }
    }
    return max;
};

Conclusion

That’s all folks! In this post, we solved LeetCode problem #835. Image Overlap

I hope you have enjoyed this post. Feel free to share your thoughts on this.

You can find the complete source code on my GitHub repository. If you like what you learn. feel free to fork 🔪 and star ⭐ it.

In this blog, I have tried to collect & present the most important points to consider when improving Data structure and logic, feel free to add, edit, comment, or ask. For more information please reach me here
Happy coding!